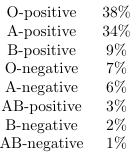Blood Type Distributions
Introduction
I was talking with a group of friends recently and somehow the topic of blood type came up. After everyone shared their blood type I was surprised to see several people had O-negative type blood. I was under the impression it was quite rare and it seemed unlikely to have multiple people with it in a small conversation. I looked up the distribution within the US population and this is what I found:
I was very surprised to see this. O type blood is the most common, with O-positive and O-negative accounting for 45% of the population combined. O-type blood is a recessive type gene and I did not expect it to be the most common. Similarly AB type blood is quite rare, which is not what I would have guessed given that A and B are both dominant genes. This is not at all what I expected the distribution to look like and I wanted to learn more. I hadn't studied biology in years, but I vaguely remembered some lectures about genetics and blood types and could do some quick googling to fill in the gaps. I wanted to understand how the distribution could look like this, and learn what about my intuition (or memory) was wrong. Rather than waste too much time with pen and paper, I decided to write a python script that would simulate multiple generations of a population reporoducing at random. Being able to tweak parameters such as number of generations or proportion of population with a given gene should really let me wrap my hands around this; however, this wasn't as straightforward as I anticipated, and the results were not what I expected.
Before diving into this though, let's brush up on a tool that will be useful for this analysis: the Punnett square
Punnett Squares
Punnett squares (devised by Reginald C. Punnett in 1905 per wikipedia) are a tool that help determine the genotypes of potential offspring when two parents reproduce. Additionally they shed some light on the probability of certain genotypes which will prove useful later on. Consider two alleles: a dominant form denoted by A and a recessive form denoted by a. Supposing we have two individuals that repdroduce, both with an Aa genotype, we get the following Punnett square:
Recalling that an Aa pair will express the dominant phenotype in the offspring, we see that 75% of the offspring will show the dominant trait whereas only 25% will show the recessive trait. Armed with this knowledge, let's return to blood types.
Positive or Negative
The "positiveness" of your blood is determined by the presence or absence of certain antigens on your red blood cells, namely any one of several Rh-Antigens. A quick google search show this is actually quite complicated, but for simplicity we can (more or less) assume that the presence of any of these antigens results in "positive" blood, and the absence results in "negative" blood. Additionally, "positive" blood is the dominant trait and "negative" blood is the recessive trait.
Now, given the example Punnett square above, I assumed that in the long run recessive traits would either:
-
Phase out of the population completely
-
Settle around 25% of the population
Assuming the table above is correct, 84% of the US population has a Rh-positive blood, but this is just close enough to 75% that I can kind of convince myself that it's possible this is just some random drift. Let's write some code and see if we replicate these numbers.
Population Simulation
If we want to simulate many generations of reproduction to determine long term trends for genotypes, it’s probably a good idea to lay down some assumptions:
-
Individuals pair off completely at random
-
No genotype increases the likelihood of an individual to surive and pass on their genes
-
We only have two alleles: the dominant ”+” and the recessive ”-”. +/+ and +/- pairs will result in the offspring carrying positive blood and -/- will result in negative blood.
-
Offspring are randomly decided according to probabilities determined by the Punnett square with their parents’ genotypes
-
We have a population of 10000 that group into 5000 reproducing pairs and produce exactly 10000 offspring who serve as the next generation
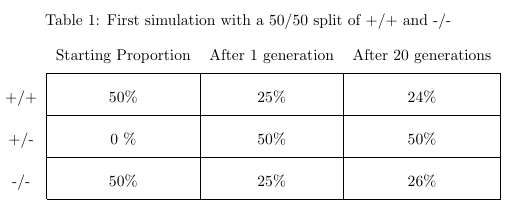
(1) and (2) are not necessarily true, and it could be interesting to alter the simulation to see how things change if we relax these assumptions. Enough of the boring stuff though, let’s see what happens if we simulate 20 generations beginning with a population where 50% of the population has the genotype +/+ and 50% -/-.
Given that +/+ and +/- express as an Rh-positive value, 75% of our population shows the dominant trait even after one generation. Let's alter the starting conditions just to verify this and move on. Just for fun let's see what happens if we make the recessive trait more prevalent than the dominant trait.
Huh. That's not what I expected would happen. We have a 55/45 split between individuals exhibiting the dominant and recessive phenotype. Not only that, but it doesn't look like there was any material change in the proportions after the first generation. What happened?
Enter The Hardy-Weinberg Principle
After some poking around on the internet, it looks like my results can be explained by the Hardy-Weinberg Principle (the same Hardy famous for "discovering" Ramanujan), which roughly states:
Suppose there are two alleles in a population: A, occuring with frequency p, and a, which occurs with frequency q. The genotype AA will occur with frequency p2, aa will occur with frequency q2, and Aa with frequency 2pq
Although it’s not the most rigorous derivation, the following Punnett square (created in microsoft paint so forgive the sloppiness) gives some intuition about where these probabilities come from:
(For those interested a slightly more rigorous derivation of these equations can be found on the wikipedia page for the Hardy-Weinberg principle and only requires some knowledge of conditional probability). The great news is that our simulations align with the probabilities in the Hardy-Weinberg principle, so we must be doing something right. The table below summarizes the results of the second simulation compared to the predicted values:
Once again, I can’t prove it rigorously, but if we were to add a third allele to our pool (such as in the case of A,B, and O alleles in blood type) I bet the expected probabilities will look very similar to the formulas in the 2 allele case. Imagine the square in figure 1 having an extra row and column, and the third allele having probability r. We would gain an r2 term in addition to two pr terms and qr terms. Some of you might recognize these terms from the following equation:
Which in turn suggests a generalization of the following sort:
Where the probability of any homozygote (e.g. +/+ or -/-) where the individual allele appears with probability pi is pi2 and the probability of a heterozygote where the two alleles occur with frequency pi and pj is 2pipj.
One quick point and then we can finally answer the question we sought out to at the start of this (admittedly too long) discussion: In the case of blood type, O-type is actually the recessive gene and A-type and B-type are co-dominant, meaning that someone carrying both genes exhibits AB-type blood. Additionally the gene determining +/- is distinct from the gene that determines your blood type. Now using this knowledge we can use the observed proportions of the different blood types and determine what ”seed proportions” would result in the population proportions we have today (subject to the assumptions laid out previously). As a reminder, here are the observed proportions of each blood type:
Using the formulas from above and a system of three equations (I'll omit the algebra since it isn't particularly illuminating) we can determine the necessary "seed proportions" that result in the population distribution seen today. Note that the table below contains the seed Genotypes.
Any population where the A,B, and O alleles occur with those frequencies will necessarily result in the distribution we see in our population today after just one generation. Of course this isn't the only solution that gets us the distribution we want. In fact there are no people with an AB-blood type. There are multiple starting populations that could result in the distribution we have today, and a population exclusively consisting of individuals with homozygotes matching the above proportions will suffice for answering the question. Of course this doesn't account for the difference in positive and negative blood types which complicates things somewhat; however, we can use the knowledge we've gained to alter the starting population and put an end to this.
My idea is pretty simple: split each population above into a positive and negative group with ratios that will result in the appropriate positive/split seen in the population. For example, consider just the population of the people with type O blood. Using the table above, we see that roughly 16% of the type O population has negative blood, and 84% has positive blood. We can once again apply Hardy-Weinberg to determine how to split the population between positive and negative in order to achieve the long run ratio seen in the population. The algebra to do this is left as an exercise to the reader, but here are the follow "seed proportions" that will result in a long run population equilibrium matching the current US distribution.
As you'll notice you can add the percentages for each blood type (i.e. AA/++ and AA/--) and you'll get the percentage seen in table 5. Of course this is not by accident, but by design. Additionally there are no people with AB-type blood in the initial population. Truth be told I wasn't sure whether or not the proportions would work out, particularly when it came to maintaining the ratio of positive to negative blood within the AB-type population, but it seems as though we got lucky. At this point, I’m satisfied with our answer to the question and ready to move on.
Final Thoughts
The real genetics behind blood types are much more interesting (and complex) than what we’ve outlined here, but it’s always interesting to attempt (and usually fail) to derive things we see in the real world and relearn some things from school. I remember reading years ago that almost nobody in China has Rh-Negative blood (roughly 3 in 1000) whereas roughly 16% of the US population has it, and now I see how this can be possible. Additionally it’s interesting that O-type blood is the recessive blood type and yet is the highest proportion seen in the US. I swear I read that it used to be the only blood until mutations resulted in the other blood types about 20,000 years ago, but I can’t find a good source at the moment so take that with a grain of salt. Fun fact I learn reading about all of this: the trait of having six fingers is the dominant trait with regards to number of fingers, and very few people seem to exhibit this trait (the same can not be said for cats, particularly in the Florida Keys). I would have thought this made absolutely no sense until creating this simulation, but now I see how this can be the case.
For anyone so inclined, I do think there are a number of interesting steps you could take to build on this analysis. My first thought: what would happen to the long run proportion of the recessive allele in the population if possessing the negative trait either killed you or greatly reduced your chance of survival. For example, what if everyone with negative type blood died before reaching adulthood? I don’t think the negative allele would disappear from the population entirely (since individuals with a +/- genotype would be fine), but I don’t think it would match the long run proportion predicted by Hardy-Weinberg.
Finally: I genuinely didn’t anticipate for this ”experiment” to get so out of hand but I feel I learned a lot. I truly thought the simulation was going to go exactly as I expected and I would have gotten bored with it in a half hour or so. I’m very happy that wasn’t the case, and now I know way more about blood types and genetics than I ever thought I would. Also I apologize for the images crudely pasted into this writing. As time I goes on I should learn how to integrate these into documents better. I was very eager to get something up though, crude tables be damned, so for right now it will have to do.
Next Time…
I recently stumbled across some notes from undergrad on how to estimate the temperature of the sun with just a ruler. Keep an eye out for that in next several days.