Calculating the Temperature of the Sun Using a Ruler

1 Introduction

A physics professor of mine in college told us a (likely apocryphal) story about a Russian physicist long ago who was very picky about who he would take on as Ph.D students, only selecting the students he felt were the best and brightest. According to my professor, he managed to select his students by having them answer one question: tell him the surface temperature of the Sun using only a ruler. On the surface this seems patently absurd. How on Earth could this be possible? There’s just no way you could possibly discern something like this with using only a ruler.

Although I doubt this anecdote about a Russian Physicist is actually true, it’s a fascinating exercise that is absolutely possible (to some extent) using only a ruler and the knowledge available to someone pursuing a Ph.D in physics. Of course we can’t determine the exact temperature, but you can get surprisingly close. Making a few assumptions and estimations that aren’t completely unreasonable, we’ll see that you can get a figure in right order of magnitude. Of course we could just look up the temperature of the sun in a textbook, but what’s the fun in that.

2 Black-body Radiation

It shouldn’t come as a surprise that we’ll need to understand how heat is emitted from the Sun and absorbed by the Earth. After some reading, it seems like black-body radiation is a good place to start. According the wikipedia, a black-body is an idealized opaque, non-reflective body in thermodynamic equilibrium with its surroundings. In turn, black-body radiation is the thermal electromagnetic radiation emitted by such a body. Although true black-bodies do not really exist, it turns out that planets and stars can be treated as black-bodies with little error in the resulting calculations. This is a key assumption to make, because black-bodies exhibit nice behavior and more importantly they emit radiation proportional to their surface temperature. This seems like a very promising lead, although it’s still not at all clear how we’re going to measure radiation with our ruler.

3 Stefan-Boltzmann Law

As we dive deeper into black-body radiation, we come across a law that will prove very useful: $\textit{the Stefan-Boltzmann Law}$. This is the law that dictates the $\textit{radiance}$ of a black-body, or the power emitted per unit area. Stated in SI units (whenever physics is involved I'll default to metric thank you) this would be: $$ \frac{watts}{meter^{2}} = \frac{joules}{meter^{2} \cdot second} $$ (I find it very helpful to keep track of units when trying to get my hands around a concept or idea. It looks like radiance is giving us a rate at which energy is emitted from a black-body per unit area, and this will be good to keep in mind when we start getting into some calculations.) And the law itself states: $$ Radiance_{black-body} = L = \sigma T_{black-body}^{4} $$ Where $\sigma$ is the $\textit{Stefan-Boltzmann constant}$, which has the value: $$ \sigma = \frac{2\pi^{5} k_{b}^{4}}{15h^{3}c^{2}} = 5.5670374 \cdot 10^{-8} \frac{W}{m^{2}K^{4}} $$ Where $k_{b}$ is Boltzmann's constant, $h$ is Planck's constant, and $c$ is the speed of light. I'll save it for another post, but I'd love to do a deeper dive into this constant. I can't recall ever seeing a $\pi^{5}$ term (or a fifth degree term for that matter) in any constant or formula and I'd love to learn where that comes from. I'd encourage readers to look more into some of these topics. The Stefan-Boltzmann law appears to be a special case of a more general law called Planck's Law of Blackbody Radiation, which provides radiance as a function of the black-body's temperature and the frequency of a desired electromagnetic radiation. Then we can integrate over all possible frequencies to obtain a closed form expression in terms of just temperature (i.e. the Stefan-Boltzmann law). Note that the general formula also accounts for the angle at which the area emits the radiation and scales it back by a $cos(\theta)$ term, but we're getting very sidetracked (something I'm often guilty of). We now have enough tools to start doing some math.

4 Deriving a closed form expression for the temperature of the sun

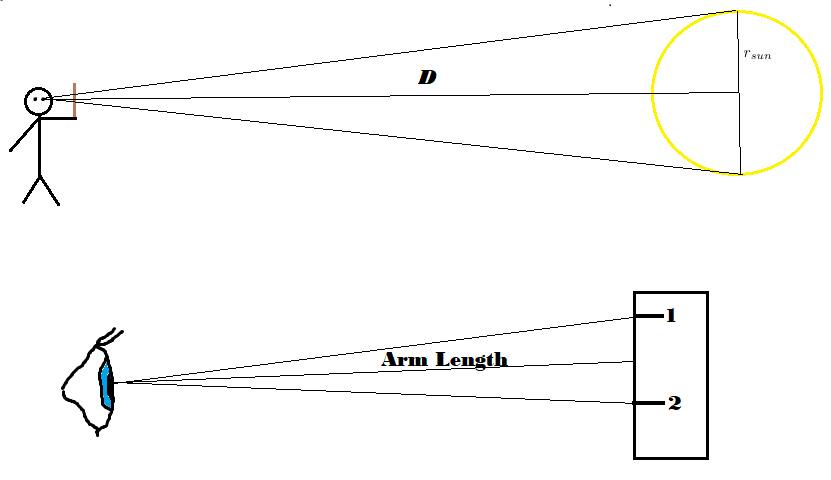
Alright, now that we have a fancy new law, let's do some math. First, the radiance of the sun of the sun according to the Stefan-Boltzmann law: $$ L_{sun} = \sigma T_{sun}^4 $$ Of course we don't know the temperature of the sun, but let's press on and hope things cancel out. Now keeping in mind that this is the wattage emitted per unit area, it might be useful to consider the total wattage emitted by the sun. Recalling the formula for the surface area of a sphere ($4\pi r^{2}$) we get: $$ Total\ Radiance\ of\ Sun = L_{sun}\cdot sun\ surface\ area = 4\pi \sigma T_{sun}^4 r_{sun}^{2} $$ (Please forgive the bad kerning in the word surface) Alright, now is where things are going to get good. Note that the figure above is the number of joules emitted by the entire surface of the sun per second (we can kinda disregard the time aspect of this for right now). As this "frontier" of energy propagates through space (i.e. moves toward other planets) its strength per unit area diminishes since the sphere of energy expands, $\textit{but the total energy remains fixed at}$ $4\pi \sigma T_{sun}^4 r_{sun}^{2}$. This means that if the Earth is a distance $D$ from the Sun, the effective energy per unit area is: $$ Effective\ Radiance\ at\ Distance\ D = \frac{Total\ Radiance\ of\ Sun}{Surface\ Area \ of\ sphere\ with\ radius\ D} = \frac{4\pi \sigma T_{sun}^4 r_{sun}^{2}}{4\pi D^{2}} = $$ $$ \frac{\sigma T_{sun}^4 r_{sun}^{2}}{D^{2}} = \sigma T_{sun}^4 \left( \frac{r_{sun}}{D} \right)^{2} $$ We seem to be making some good progress, and we finally got to cancel our first terms in the most recent calculation which is always a good feeling. Also note that the above is once again a measure watts/unit area. This will prove useful in a moment. Moving on, we now need to consider what happens from the Earth's point of view when the energy reaches it. If we continue imagining the "frontier" of energy that propagates outward from the sun each second, we can envision the Earth punching an Earth sized hole (i.e. absorbing a fraction of the energy emitted by the sun) in this energy frontier. Thinking about it a little, we see that the Earth takes a chunk out of the boundary equal to its $\textit{cross-sectional area}$, not its surface area. Well how much energy is this? Let's see: $$ Total\ energy\ hitting\ the\ Earth = Cross\ sectional\ area\ of\ Earth \cdot Effective\ Radiance\ at\ Distance\ D = \frac{\sigma T_{sun}^4 r_{sun}^{2} \pi r_{earth}^2}{ D^{2}} $$ And of course we could distribute this over the entire surface area of the Earth to obtain the average energy absorbed per unit area. $$ Average\ energy \ per \ unit \ area = \frac{Total\ energy\ hitting\ the\ Earth}{Surface\ Area\ of\ Earth} = \frac{\sigma T_{sun}^4 r_{sun}^{2} \pi r_{earth}^2}{D^{2}}\cdot \frac{1}{4\pi r_{earth}^2} = \frac{\sigma T_{sun}^4 r_{sun}^{2}}{4 D^{2}} $$ We have one final trick up our sleeve before we're in the home stretch. We will assume that the Earth is a black-body in equilibrium, meaning that the energy it radiates is equal to the energy it takes in. Recalling the Stefan-Boltzmann law we now have: $$ Energy\ absorbed\ by\ Earth = Energy\ radiated\ by\ Earth $$ $$ \frac{\sigma T_{sun}^4 r_{sun}^{2}}{4 D^{2}} = \sigma T_{earth}^{4} $$ Rearranging and cancelling some terms we finally obtain: $$ T_{sun}^{4} = T_{earth}^{4}\frac{4D^{2}}{ r_{sun}^{2}} $$ $$\text{or}$$ $$ T_{sun} = T_{earth}\sqrt{\frac{2D}{ r_{sun}}} $$ Finally we can see the light at the end of the tunnel. We have an expression for the temperature of the sun as a function of the temperature of the Earth, and we can determine everthing else in the expression. "But wait, how do we know the distance from the Earth to the Sun, or the radius of Sun? We still have to find those!" You say. Well the truth is, we don't know those things, there's no math left to be done that might cancel those terms out, and we certainly don't have the tools to measure them directly. Thankfully though we don't need to know those things $\textit{individually}$. Using our old friend geometry we can estimate their $\textit{quotient}$ using, yes, a ruler.

5 Similar Triangles

It’s a little tough to explain what’s going on here, but I was kind enough to create the following diagram to try and explain how exactly we’re going to use the ruler.

Figure 1: Diagram Illustrating Ruler Use

In the top part of the image, we see someone holding the ruler arm's length away in such a way that they can "measure" the "height" of the sun. I've labeled the image to show how doing this creates a triangle with a height equal to $D$ and base equal to $r_{sun}$ Now looking at the bottom diagram, we see there is a second triangle formed at the same time $\textit{that looks awfully similar}$ to the first one. In fact, not only do these triangles look similar, they are mathematically similar! The proof of this fact is left as an exercise to the reader, but trust me that the angles in both triangles are equal (despite what it might look like in the figure). This is great news because now that we know the triangles are similar, we know the following: $$ \frac{D}{r_{sun}} = \frac{\text{arm length}}{1/2 \text{measured "height" of the sun}} $$ And we can easily measure the values on the right hand side, meaning we can obtain a value for the quotient on the left hand side. This is now all of the info we need to complete the formula above and get an estimate for the temperature of the sun. Let's do some measuring and put this matter to rest.

6 Putting it all together

Recall our formula from earlier: $$ T_{sun} = T_{earth}\sqrt{\frac{2D}{ r_{sun}}} $$ My attempt to measure the "height" of the sun ended up burning my eyes quite a bit, but I obtained a value of roughly 0.4 inches for the height of the sun, and my arm length as roughly 28.5 inches (the unit we masure these in doesn't matter since the quotient would be the same in any unit system). As a final quick note, we do need to plug something in for the average temperature of the Earth. For no particular reason, I'll go with an average of 0 degrees Celsius, or 273.15 Kelvin (we have to use Kelvin in the formula below and then we can convert back to Celsius or Fahrenheit). Might sound low to some people but I have a feeling this is closer to the truth than you might think. (Of course this is nothing more than an educated guess and we'll see in the end that the final figure isn't too sensitive to our estimate.) Plugging our values into the above equation we get: $$ T_{sun} = (273.15\ K)\sqrt{2 \cdot \frac{28.5}{0.2}} = 4611.3\ K $$ 4611 degrees Kelvin, which sounds hot but not as hot as I would have thought. A quick google search shows that the actual temperature of the surface of the sun (note that the area surrounding the sun is much hotter and I'm not sure we understand why just yet) is a bit hotter, roughly 5778 K. So all things considered not bad, and as it turns out we can improve our estimate with a little more research. Remember when we assumed the Earth was a black-body that absorbs all the radiation from the Sun that hits it? Well it turns out that's not entirely true. The sun emits quite a lot of radiation with high frequencies (somewhere in the ultraviolet part of the spectrum) that gets reflected off the Earth. This is known as \textit{albedo} (derived from the Latin for whiteness apparently), and it is typically represented by $\alpha$. Consequently, the Earth only absorbs a portion, $(1- \alpha)$, of the radiation that hits it. Recall from above that we equated radiation absorbed by the Earth to radiation emitted by the Earth. We can alter the radiation absorbed half of the equation to obtain the following: $$ \frac{(1-\alpha)\ T_{sun}^4 r_{sun}^{2}}{4 D^{2}} = T_{earth}^{4} $$ Solving for $T_{sun}$ like we did above yields: $$ T_{sun} = T_{earth}\sqrt{\frac{2D}{ r_{sun}\sqrt{1-\alpha}}} $$ I will admit that introducing this term brings some additional complexity into the picture. How exactly can we estimate it using a ruler? Well to be honest, we can't; however, we can guess what $\alpha$ might be. We know it's constrained between 0 and 1. Even better, we can try multiple values and see what we get. Here's a table showing what the derived temperatures for the sun (in Kelvin) as we vary our $T_{earth}$ guess and $\alpha$ guess.

Figure 2: Table Showing Relationship Between Estimated Earth Temperature and Calculated Sun Temperature (in Kelvin)

I recognize it's a little weird to put the estimate for Earth termperature in Celsius and resulting sun calculation in Kelvin, but I think it's a little easier to think of the Earth's temperature in terms of Celsius (for those who don't know it, the Fahrenheit conversion is 1.8*C + 32), but saw no reason to convert the calculated temperature from Kelvin back to Celsius (especially since the Kelvin and Celsius figures tend to be pretty close once we're in the thousands). Anyway, looking at our table we see some interesting things. First, the range of calculated temperatures is not unreasonably wide, spanning from 4274 K to 7400 K. (I recognize that 7400 is nearly double 4274, but again I think all things considered this is pretty close. It's not like our range is 2000 K to 150000 K.) It might be tough to calculate the exact figure this way, but I feel very confident that the surface temperature is somewhere in the low thousands based on these results (as opposed to say somewhere in ten thousands, millions, or even billions). Second, note the range in temperatures for any particular column. If we vary our initial temperature guess of the Earth by as much as 40 degrees Celsius, we still see final estimates in roughly the same ballpark. (Of course the clever reader knows this is because we ultimately input these temperatures in Kelvin, and a change of 40 K isn't that large from a percentage standpoint when our input temperatures are in the mid to high 200's). The Earth's actual albedo value is roughly 0.3, which corresponds to a calculated surface temperature of roughly 5000 K. Still below the actual value, but I won't lose any sleep over it considering the methodology.

7 Final Thoughts

I recognize this calculation is far from perfect, and this method will never be able to get you anywhere close to the actual temperature of the surface of the Sun. For instance in neglects to account for the greenhouse effect in any capacity and assuming the Earth behaves as a black-body does throw off some of the calculations;however, I don’t particularly care about these as that wasn’t exactly the point of the exercise. Through the use of the Stefann-Boltzmann law, we were able to derive a closed form expression for the temperature of the Sun relative to the temperature of the Earth, and the estimate we got ended up being pretty good! It’s interesting to investigate the laws we learn and how to apply them. Furthermore, I forgot how interesting space can be and have loads of new questions I’d like to look more into. Such as:

1. How do we actually calculate the temperature of the sun? I honestly have never thought about this before and wonder how it’s done. Might be interesting to see if any methods can be done with few tools.

2. How is the Stefann-Boltzmann constant calculated? I’ve been thinking more about this and would really like to know. I have convinced myself that the π⁵ term is the result of integrating an expression with a fourth-degree term (note that the denominator is also divisible by 5) but otherwise I genuinely can’t see where this would come from.

3. Can we measure any of the ”big distances” in the calculations above through some other means? We were lucky that many of them cancelled out, or we were able to indirectly estimate them, but I wonder if it’s possible to calculate the number of miles to the sun directly. I think older astonomers were able to calculate a lot of these distances and I’d like to know how. Hell I think I remember that one was even able to calculate the speed of light (with decent accuracy!) based on the expected time a moon of Jupiter was supposed to be visible and when it was actually visible. This sort of thing seems impossible to me. I’d love to learn more about this.

4. Why does Mercury being in retrograde last for roughly 23 days? This isn’t really at all related to what we calculated above, but someone mentioned it recently and now that I’ve got space on the mind I’m curious to investigate

5. Another not at all related to this, but how was Kepler able to calculate his laws? And how was Newton able to deduce them strictly from a few axioms? These things would have been done in the 1500s and 1600s so I’d like to believe I should be capable of replicating it.

That’s all for now though. We’ll be returning to the topic of space quite a bit, but I want to dive into some data work and computer science before returning.